Libraries, libraries, libraries.

Its all about the quantity and quality of libraries that are out there. Its why python is 'insanely great'.

Two of my favorite (in that I use them all the time) libraries are numpy and matplotlib. Anyone doing serious scientific/engineering analysis will find them invaluable.

The other day I got 20Mb of data, spread over two spreadsheets. A years worth of temperature, pressure and flow readings from a process refinery. (A single spreadsheet can only have 65000 rows, hence the two spreadsheets). Problem: determine if there are significant diurnal influences on one of the readings. And correlations between some of the others. And produce some publication quality plots of the others.

Solution (mostly with python). Cut and paste all the data into a text file. Emacs handles the quantity of data easily. Save the text file. (Non python bit done).

Now just use matplotlib. The 'load()' command gets all the data into numpy arrays. Reverse the data, since it was provided with the final data point first. Do a power spectral density 'psd{)' on the data of interest. Reshape the arrays to nx12, and average across the rows (since there is too much data to plot directly). Call plot() in various clever ways. Tidy things up. Save as pdf output. Done. Excel couldn't even handle this (and the plots is produces are crap.)

So, libraries, libraries, libraries. Its all about the libraries. Python may be slow at straight number crunching, but if you can get the data into a numpy array, you have access to highly optimized numerical methods for manipulating the results. The libraries are all out there.

Actually not just libraries. There is a vast collection of third party routines which will likely do just whatever you want. Two examples. I needed some routines for sunrise/sunset calculations for some solar energy work. 'sunrise sunset python'. JFGI. I found Henrik Härkönen had written a python class to do just this. (and added other useful stuff, like maximum solar flux).

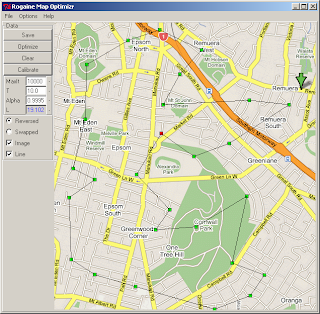
Then a few weeks back I was looking at optimizing rogaine courses. Rogaine is a form of orienteering where you have to get to as many control points as possible in some fixed time. So, what is the shortest path taking in all the control points? This is a standard example of the traveling salesman problem, and good approximate solutions can be found by simulated annealing. So 'simulated annealing python'. JFGI. Dozens of hits, often the problem is sorting out what could be useful and useable. Anyway, there is code out there to do just what I want. Wrap this in a Tkinter gui interface to display the map of interest and add control points and there you are:

Evolution of a Python programmer

It is interesting to look back at how one evolves as a Python programmer. I ran across a blog which discussed this in general terms here:

http://www.vetta.org/2008/05/scipy-the-embarrassing-way-to-code/

Now I have some actual examples of this evolution, from basically programming a direct copy from FORTRAN, to being truly pythonic. Over time it evolved into true python and here is how it happened:


So to start we have a direct translation of some FORTRAN Code for doing composition flash calculations. Solve for equilibrium composition by root bisection where the main calculation is built into subroutine

def cFlash2(X, K, nC):
    EPS = 1.0e-8
    TOL = 1.0e-6
    MAXITER = 100
    La = 0.0
    Lb = 1.0
    f0 = 0
    for i in range(nC):
        f0+=(K[i]-1)*X[i]/K[i]
    f1 = 0
    for i in range(nC):
        f1+=(K[i]-1)*X[i]
    if (f0>0) or (f1<0):
        print "No VLE"
        return -1
    print f0, f1
    for i in range(MAXITER):
        L=(La+Lb)/2.
        if abs(La-Lb)            return L
        f = 0.0
        for j in range(nC):
            kk =(K[j]-1)*X[j]/(L+K[j]*(1-L))
            f=f+kk
        if (f>EPS):
            Lb=L
        elif (f<-EPS):
            La=L
        else:
            return L

So we get a bit pythonic. Define a separate function, arrays know their size, tuples for multiple definitions. Return None if we can't find a solution

def f(L, X, K):
    fx=0
    for j in range(len(X)):
        fx+=(K[j]-1)*X[j]/(L+K[j]*(1-L))
    return fx
    
def cFlash(X, K):
    EPS, TOL = 1.0e-6, 1.0e-8
    MAXITER = 100
    La, Lb = 0.0,1.0
    f0,f1 = f(0,X,K), f(1,X,K)
    if (f0>0) or (f1<0):
        print "No VLE"
        return None
    for i in range(MAXITER):
        L=(La+Lb)/2.
        if abs(La-Lb)            return L
        fx = f(L,X,K)
        if (fx>EPS):
            Lb=L
        elif (fx<-EPS):
            La=L
        else:
            return L

Now define the function locally so we don't contaminate the global namespace and can access the function parameters. Use enumerate to access list index. Raise an exception if root can't be found.

def cFlash(X, K):
    def f(L):
        fx=0
        for j,k  in enumerate(K):
            fx+=(k-1)*X[j]/(L+k*(1-L))
        return fx
    EPS, TOL = 1.0e-6, 1.0e-8
    MAXITER = 100
    La, Lb = 0.0,1.0
    f0,f1 = f(0), f(1)
    if (f0>0) or (f1<0):
        raise VLEError
    for i in range(MAXITER):
        L=(La+Lb)/2.
        if abs(La-Lb)            return L
        fx = f(L)
        if (fx>EPS):
            Lb=L
        elif (fx<-EPS):
            La=L
        else:
            return L

Now we are using a canned Brent solver routine, which is much faster and more robust. Error handling is all in the canned routine

def cFlash(X, K):
   def f(L):
       fx=0
       for j,k  in enumerate(K):
           fx+=(k-1)*X[j]/(L+k*(1-L))
       return fx
   return solver.zbrent(f,0,1)

List comprehensions, zip, sum. Reduce FP operations in inner product term from 6 to 4 by rearrangement

def cFlash(X, K):
   def f(L):
       return sum([x/(k/(k-1)-L) for x,k in zip(X,K) if k!=1.])
   return solver.zbrent(f,0,1)

Now going *too* far: functional version using lambda

def cFlash(X, K):
   return solver.zbrent(lambda L:sum([x/(k/(k-1)-L) for x,k in zip(X,K) if  k!=1.]),0,1)

In fact, why bother with a function, just inline the call! Actually, the last version is reaching the point of being obscure and offers no efficiency gains over the previous version. The lambda is just syntactic sugar (GVR wants to get rid of it, and I probably agree, though it is useful for some callback situations where the function call is trivial and defining the function makes the code messier than just the lambda, and I do use it in Tkinter code a lot)

Final production version: precompute the ratios k/(k-1) reducing the FP count to two

def cFlash1(X, K):
   XK1 = [(x, k/(k-1.)) for x,k in zip(X,K) if k!=1]
   def f(L):
       return sum([x/(k1-L) for x,k1 in XK1])
   return solver.zbrent(f,0,1)

Anyway that sequence basically shows the progression that I have made in using python. In doing so, there have been a number of optimizations made that are transparent when you write in the functional form. The code is perfectly adequate for the present purpose, but if I needed additional speed, I would simply rewrite the core function using NumPy for the array manipulations. In that case the overall speed would approach that of compiled c++, combined with the transparency of python.

But agreed, looking back at ones old code can be embarassing!

The most useful function we never learned at school

In school math we learned all about sin() and cos() and tan() and log() and a few other trigonometric and special functions. But one of the most useful functions I have ever come across never got taught and perhaps it should.

I have programmed variants of this function in just about every language I have ever programmed in, and I use it all over the place. And it is a function that has applications in real life in just about every field.

The function is just a linear map. If we have something that takes one value at some time and a different value at another time, and the value is changing in the simplest possible way between the two times (ie linearly), what is the value at some intermediate or later time.

In general, if we have a linear function of a variable x with value y1 when x=x1 and value y2 when x= x2, what is the value in general?

A long time ago (ie FORTAN days), I would write a function

y = li(x, x1, y1, x2, y2)

with five parameters and then call this whenever I wanted to map from world to screen coordinates or any other application. Now very often I want to have the same linear map available for many many calls (like in doing computer graphics), so I would end up writing another function

y = li1(x, a, b)

where I could precompute a and b. Or even keeping a and b as global variables, setting them and just being able to call a function with a single parameter.

Now fast forward to Python. I figured out early on I could just do this

def li(x1,y1, x2,y2):
   b = (y2-y1)/(x2-x1)
   a = y1 - x1*b
   def f(x):
       return a+b*x
   return f

so then I could create a function taking only a single x value and evaluate that to my hearts content:

>>> f = li(0., 3., 1., 2.)
>>> f(4)
-1.0
>>> f(2)
1.0
>>> f(1)
2.0
>>> f(0)
3.0
>>>

or if I wanted a single call

y = li(2., 2., 3., 5.)(4.5)

Apparently I had discovered closures, which turn out to be a good thing in functional languages and computer science. My li() function (LinearInterpolate) sets up a closure, encapsulating the parameters, and allows the actual function to be called while keeping these values (in this case the precomputed intercept and slope, for those who did traditional cartesian geometry at high school)

Anyway, this linear map function turns up all over the place in coding and is such a useful animal that it should be taught in school. Trigonometry has its uses but straight linear mappings are probably much more common in real life! If you bank balance is $335.47 in January and $221.38 in March, and you don't change your spending or earning habits, what will it be in September?

>>> lin(1, 335.47, 3, 221.38) (9)
-120.89
>>>

So it is likely that you will change your spending habits (unless you have arranged an overdraft)

Enumerating Bracelets

This is only vaguely python related, in as much as it shows one useful facet of the language: we never have to worry about integer overflows. Python will use ordinary integers if it can, but if numbers get too large it will transparently switch to a "big integer" with size limited only by memory and computing resources..

The problem is this (for a simple case)

Given a single diamond, ruby, sapphire and an emerald, how many different
bracelets (or necklaces) can we make using any number and combination of the gems? We consider
two bracelets identical if they are congruent under some combination
of rotation or reflection.

Thus the following are considered to be identical bracelets:




while the following, although comprising the same jewels, are
different:


For this particular case (four jewels) we can enumerate all the possible cases. If we just attach a single jewel there are four possibilities: it can be a ruby, emerald, sapphire or diamond, for two jewels we have six possibilities, for three jewels there are just four: we can exclude any one of the gems and then no matter how we order the other three, the result is identical

With all four gems, the order matters, but there are only three distinct patterns: the ruby can be opposite the diamond, sapphire or emerald, and we can flip the other two to get these cases.

For completeness we include the empty case, tough do not under any circumstances give this to your spouse as an anniversary gift no matter how understanding they may be of mathematics and the importance of the null set.



So we find a total of eighteen possibilities in all.


Now if we calculate the number for different values of n (the number of distinct jewels) we find:

f(0) = 1
f(1) = 2
f(2) = 1+2+1 = 4
f(3) = 1+3+3+1 = 8
f(4) = 1+4+6+4+3 = 18
f(5) = 1+5+10+10+15+12 = 53
f(6) = 1+6+15+20+45+72 = 219

The sequence continues

1, 2, 4, 8, 18, 53,219, 1201, 8055, 62860, 556070,
5488126, 59740688, 710771367, 9174170117...

It is pretty straightforward to find a formula for the series:




In Python,

def ffact2(n):
  tot = 1+n+n*(n-1)/2
  k = n*(n-1)
  for i in range(n-2, 0, -1):
      k*=i
      tot+=(k/(2*(n-i+1)))
  return tot

Now a bit of analysis suggests that:



To check this out all we need to do is take a factorial function and do a few quick calculations:

def fact(n):
  if n==0:
      return 1
  else:
      return n*fact(n-1)

def ff2(n):
  return ffact2(n)*2/(float(fact(n-1)))/(1+1./(n-1)*\
  (1+1./(n-2)*(1.+1./(n-3))))

for i in range(4,50): print ff2(n)

and we get

3.6
3.21212121212
2.88157894737
2.76091954023
2.72865853659
......
2.718282524
2.71828246475
2.71828241167

which is nicely converging on e, demonstrating the conjecture. Now the point of all of this is how easy it is to do this in Python. Try the same thing in any compiled language and you will start to get integer overflows! We calculated factorials of some very large numbers and never had to worry about the fact that integers might overflow. Python takes care of this automatically, since ordinary and big integers are unified in the language.

The Weather here...

OK, part of the problem here is that I have so much stuff and it is difficult to get started. The weather is always a good subject to get a conversation going and it is quite t(r)opical at the moment.

I live in Central Queensland, and we are in the middle of the wet season. (Also the hurricane/cyclone season, but they are fortunately pretty rare in these parts, and even when they happen, well Cyclone Larry a couple of years ago was about a thousand km north of here, and I had to explain to American friends who called concerned about my wellbeing that this was the equivalent of a Florida hurricane if you lived in Virginia)

On the other hand we get severe thunderstorms and associated hail so it is useful to keep a watch out for what is going on so that you can move your car inside. (One of our friends who is a car dealer lost seventy vehicles in a hailstorm once...)

Anyway, there is a local weather radar on the Bureau of Meteorology weather site, which displays an updated weather picture every ten minutes. You can leave your browser open and keep an eye on things. However to really get a feel for which way the weather is coming, it is better to watch a loop, and they provide this too, but only four recent images. I wanted to watch the longer term development of storm systems, so here is the answer:

import time, urllib
rfile = "IDR233_%03d.gif"
dataFile  = "http://mirror.bom.gov.au/radar/IDR233.gif"
i=1
while 1:
    urllib.urlretrieve(dataFile, rfile % i)
    i+=1
    time.sleep(600)

The image I want to download is the same each time, but I want to save it to a series of images that I can replay, so I generate a unique new filename each time, hence the counter. Apart from that, there isn't much to see here, its just eight lines of code that took a couple of minutes to write. Here is the result, a few frames put into an animated gif showing a major thunderstorm approaching Gladstone:



Now my original intention with this blog was to talk about a whole lot of interesting scientific and engineering applications for Python, so why am I starting off with what is a very trivial web application? Because Python (batteries included) has this stuff as standard libraries and easy to use. And since it is there, I learned how to use it. I may not use it much, but it has given me insight into other areas of computing (this internet web series of pipes thingy that everyone seems to be on about
these days.

So Python is keeping me learning and that is insanely great.

Incidentally, I learned how to use the urllib stuff from working through the Python Challenge website. Its a very useful collection of little problems that introduced me to the more web-centric use of the language: a different erspective on the language to the engineering issues I generally deal with.

Motivation

So where do we begin? Well with how this blog came about...

I have been thinking about writing some of this stuff down for some time, but a few recent Python related posts have motivated me to getting out and having my say on the matter. A few weeks back was this XKCD cartoon
which probably sums up how us enthusiasts feel about the language.
Welcome to our world, Randall.

But just yesterday I noticed this entry that said Knuth had suggested using indentation for program structure many years ago. Since one of the perennial bugbears that arises in Python advocacy is the use of significant whitespace, having DEK's seal of approval puts the final nail in the coffin of the naysayers. The Knuth books have been a source of information and inspiration to me for many years and I have pored over every line and worked through most of the exercises in search of a mistake (motivated by the desire to score one of the checks). I did find one mistake a few years ago but I had been beaten to the punch by a few months as it turned out. I did manage to get a $0.32 'valuable suggestion' check last year by solving one of the problems in a new and different way, and Python was instrumental here. More on that sometime in the future, it is a good story and demonstration of the power of the language.

The bottom line is: suck it and see. The use of whitespace indentation
for structure is elegant. You will get used to it. ESR did along with many others.

I won't go over the interminable arguments that are raised against whitespace structure. For me, the indentation makes code readable and unambiguous. It just works (for me anyway). End of story. And as I said in the previous entry, for an old FORTRAN user, it never was an issue.


The indentation works as does the language as a whole. (Again, for meanyway). This may be related to the sort of engineering/scientificproblems I tackle and the environment in which I work. The librariessupplied with Python cover just about everything I need and it is easy tofill in the gaps. Speed is never an issue: for number crunching onhomogeneous arrays we have Numpy, and if there is anything which can't bemodelled there, swig is your friend. Or ctypes. The possibilities are endless.

Anyway, I digress. Seeing the whitespace issue raised yet again just made me feel it would probably be worth putting in my $.02 worth. So here we are.

So enough motivation and advocacy for the time being. I'll try and address some interesting problems that I have solved efficiently using Python. The sort of problems of interest to an engineer/scientist working with real world issues. I have yet to find any real reason to become au-fait with closures, functional programming and a lot of the other topics that get discussed in some of these forums (forii?) Python may or may not handle these but it is certainly good for useful (to me) stuff.

Python Homecoming...

After about thirty years of wandering around the planet, living and working on four continents I recently settled back to a small beachfront town in Australia, the country where I was born.

And after over thirty years of wandering among computer languages I have finally settled on one that I feel will last me for the rest of my career.

The language is Python, and using it makes me feel like I have come home: hence the title of this blog.

I started with FORTRAN on punched cards many years ago. And with Python, I can still write FORTRAN if I need to. Both literally and figuratively as I will get around to discussing.

Most of my software development is numerical algorithmic in nature: my code tends to consist of long series of primarily numerical expressions interspersed with logic. So Python is the closest language I have found to FORTRAN when it comes to writing numerical expressions. And one regular but ill-judged complaint about Python - its use of indentation as a structuring mechanism - is no obstacle to anyone who grew up with FORTRAN!

FORTRAN:

y = x**5 + sin(z)

python:

y = x**5 + sin(z)

compared to

tcl:

set y [expr {pow($x,5) + sin($z)}]

c++:

y = pow(x,5)+sin(z);

So my software environment started with FORTRAN, moved to C in the early 80's, then to C++. There were various side excursions: FORTH, Pascal and Java came and went. Along the way I became aware of scripting languages, which were an easy way of doing a lot of things that didn't need the full power of a compiled language and let you make GUI's for applications with comparative ease. I started with Tcl/Tk, had an occasional foray with perl, but when I came to do a fairly major project, I picked on Python for the job because it seemed like a good language with class and GUI support, and particularly well documented.

I learned the language, finished the application and never looked back. Python has let me solve a lot of interesting problems, write a number of useful applications, got me a Knuth check and generally made life easy. I figure I am 'retired' now, I don't need to learn any new languages because there is more than enough new useful stuff still going on in the Python world to keep me interested.

Anyway, this blog will talk about the history of how I ended up coming home to Python, undertake a bit of advocacy, and generally be a post for interesting and useful (to me) stuff that I run across in my daily work. The emphasis will be on numerical/analytical techniques rather than hardcore language issues.


And I enjoy Monty Python as well! Thanks Guido for giving us this wonderful language.